二叉搜索树

Posted on | In
Words count in article: 723 | Reading time ≈ 3

主要介绍了二叉搜索树的遍历，查找，最小(大)结点的查找，前驱结点，后继结点，插入新结点，删除结点等操作的实现

基本介绍

满足如下特点的二叉树: 设x为二叉搜索树中的结点。如果y是x左子树中的一个结点，那么y.key <= x.key。如果y是x的右子树中的一个结点，那么y.key >= x.key

基本操作(伪代码，摘自算法导论第12章)

中序遍历

1
2
3
4
5
INORDER-TREE-WALK(x)
    if x != null
        INORDER-TREE-WALK(x.left)
        print x.key
        INORDER-TREE-WALK(x.right)

查找

1
2
3
4
5
6
TREE-SEARCH(x, k)
    if x == null or k == x.key
        return x
    if k < x.key
        return TREE-SEARCH(x.left, k)
    return TREE-SEARCH(x.right, k)

最小结点查询

1
2
3
4
TREE-MINIMUM(x)
    while x.left != null
        x = x.left
    return x

最大结点查询

1
2
3
4
TREE-MAXIMUM(x)
    while x,right != null
        x = x.right
    return x

后继结点

1
2
3
4
5
6
7
8
TREE-SUCCESSOR
    if x.right != null
        return TREE-MINIMUM(x.right)
    y = x.p
    while y != null and x == y.right
        x = y
        y = y.p
    return y

前驱结点

1
2
3
4
5
6
7
8
TREE-PREDECESSOR
    if x.left != null
        return TREE-MAXIMUM(x.left)
    y = x.p
    while y != null and x == y.left
        x = y
        y = y.p
    return y

插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
TREE-INSERT(T, z)
    y = null
    x = T.root
    while x != null
        y = x
        if z.key < x.key
            x = x.left
        else x = x.right
    z.p = y
    if y == null
        T.root = z
    else if z.key < y.key
        y.left = z
    else y.right = z

删除

  • 子过程TRANSPLANT，用来用另一棵树替换一棵子树，并成为其双亲的孩子结点

    1
    2
    3
    4
    5
    6
    7
    8
    TRANSPLANT(T,u,v)
        if u.p == null
            T.root = v
        elseif u == u.p.left
            u.p.left = v
        else u.p.right = v
        if v != null
            v.p = u.p

  • 删除结点

  1. z结点只存在左子树
  2. z结点只存在右子树
  3. z结点存在左右子树
    3.1. z结点的后继结点y为z的直接右孩子
    3.2. z结点的后继结点y不是z的直接右孩子

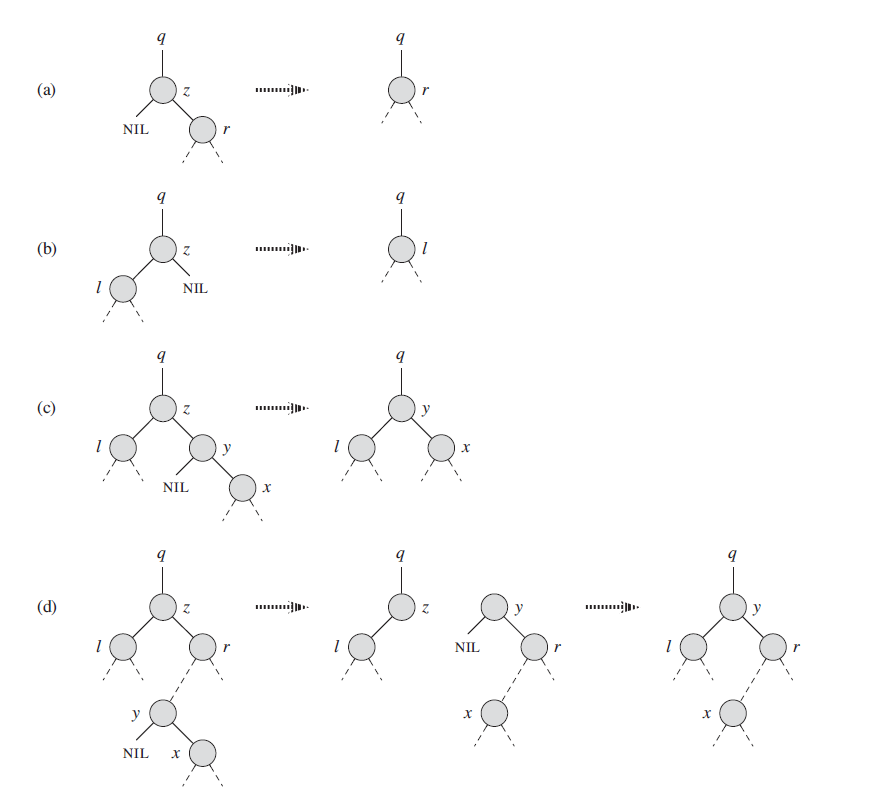
tree-delete-img

实现伪代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
TREE-DELETE(T, z)
    //1:如果z结点的左子树为空，则直接用z结点的右子树替换z原来的位置
    if z.left == null
        TRANSPLANT(T,z,z.right)
    //2:如果z结点的右子树为空，则直接用z结点的左子树替换z原来的位置
    elseif z.right == null
        TRANSPLANT(T,z,z.left)
    //3:z结点左右子树都不为空
    else y = TREE-MINMUM(z.right)//获取z结点的后继结点y
        //3.1: 如果y结点不是z结点的右孩子，则用y的右子树替换y原来的位置，并且设置y结点为原来右子树的父节点
        //说明: 如果y结点为z的后继结点，则y结点肯定不存在左子树
        if y.p != z
            TRANSPLANT(T,y,y.right)
            y.right = z.right
            y.right.p = z.p
        //3.2 用y子树替换掉z子树原来的位置，并设置z结点的左子树为y的左子树
        TRANSPLANT(T,z,y)
        y.left = z.left
        y.left.p = y

参考资料

  • 算法导论第12章